The Magnet 097: Four Bugs, Fake Sandos, and Butter Stink

Mathematical Games, Misrepresented Food, and Manga Masterpieces

Using Ai to Animate the Four Bug Problem

Lately, I've been having fun experimenting with an AI coding editor called Cursor. It has many professional features, such as integration with developer tools and predictive editing. However, since I don't really know how to code, I primarily use Cursor's natural language code generation. This feature allows me to describe what I want in plain English, and then Cursor generates the corresponding code.

Here’s an example of a recent program I asked Cursor to write for me: “The Four Bug Problem.” It first appeared in the November 1957 issue of Scientific American in Martin Gardner’s “Mathematical Games” column:

The Four Bug Problem illustration from the November 1957 issue of Scientific American.

Here’s how Gardner stated the problem:

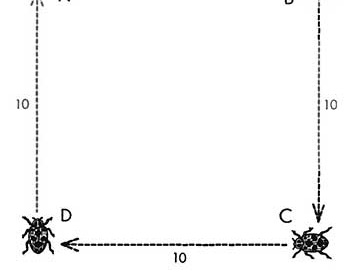
Four bugs — A, B, C and D - occupy the corners of a square 10 inches on a side. A and C are male. B and D are female. Simultaneously, A crawls directly toward B, B toward C, C toward D, and D toward A. If all four bugs crawl at the same constant rate, they will describe four congruent logarithmic spirals which meet at the center of the square. How far does each bug travel before they meet? The problem can be solved without calculus.

(I’m not sure why he had to say that the bugs were male and female — maybe to give the bugs a reason to pursue each other?)

Gardner revisited the Four Bugs Problem in the July 1965 issue of Scientific American, and this time, it was featured as the striking cover image:

July 1965 cover of the Scientific American.

The issue’s description of the cover also included the puzzle’s solution:

The Op-art pattern on the cover, a set of nested and rotating squares, is an example of the close relation of such patterns to many problems encountered in recreational mathematics (see "Mathematical Games," page 100). This painting illustrates the "four-bug problem." The bugs start at the corners of a square. Simultaneously they begin to move clockwise, each crawling at the same speed and each heading always for its neighbor. At any moment the bugs mark the corners of a square that becomes smaller and rotates as they crawl. Each bug's path (shown here in the appropriate color) to their meeting point in the center is a spiral the length of which is exactly equal to a side of the original square.

I thought it would be fun to see if I could use Cursor to recreate the cover art. I told it I wanted it to write a web app that recreated the famous four-bug problem and drew colored lines connecting the bugs as they pursued each other. It took a few iterations to produce what I wanted, but in less than 20 minutes I had a nice little demo. Check it out here.

I used Cursor to create this Four Bug problem demonstration.

I'm having such a great time with Cursor that you'll probably see more of these demonstrations in future issues of the newsletter.

By the way, Scientific American often featured Gardner's puzzles on its covers. Here are some other examples.

---

7-Eleven Is Lying to You About the Japanese Egg Salad Sandwich Coming to America