The Magnet 099: The Homicidal Chauffeur Problem

How game theory mathematics shaped military strategy during the height of the Cold War

"The only winning move is not to play." From the 1983 film WarGames

How could anyone resist reading a Wikipedia article titled “Homicidal Chauffeur problem?” I couldn’t! I learned that it was a math problem posed in 1951 by game theorist Rufus Isaacs in his paper for the RAND Corporation called “Games of Pursuit.”

The problem takes place in a parking lot, empty except for a person on foot (the evader, designated by the letter E) and a homicidal chauffeur (the pursuer, P) who wants to run over the evader. P is faster than the E, but E can make tighter turns while running. With E’s “only hope being delay until rescue,” what is the best strategy to avoid being run over?

“Some qualitative aspects are evident,” wrote Isaacs. “If E is more or less in front of P the situation is simple; E will flee and P will follow.” Because P is faster, E is doomed.

Illustration of the Homicidal Chauffeur problem from Rufus Isaacs’ 1951 paper, “Games of Pursuit.”

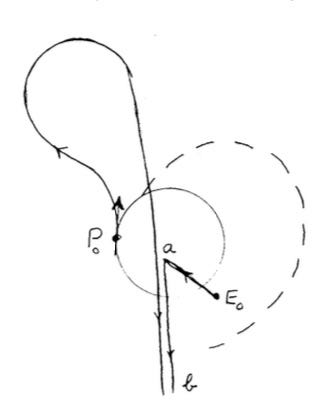
But what if the chase begins with the evader behind the pursuer? Isaacs included a hand-drawn illustration in his paper to explore this scenario (shown above). P₀ and E₀ are the starting positions of the pursuer and the evader. If E can get inside the circle of P’s turning radius (shown in the figure as the solid circle), they can avoid being hit. But if P is smart enough to first turn away from E and “then swerve about and pursue directly,” then E will have to run toward P in an attempt to stay inside the car’s turning radius. “But as P starts to swerve, E (now at [.a]) turns tail and flees until capture is consummated near b.”

To determine E’s best strategy for staying alive as long as possible, Isaacs developed a solution that started with the desired outcome and worked backward to find the optimal strategy — the best moves for both pursuer and evader where neither can do better by changing their approach. This is called a “Nash equilibrium” in game theory.

Origins of Game Theory

The RAND corporation wasn’t interested in helping people learn how to evade homicidal chauffeurs. They were interested in military problems, like how a nimble fighter jet could outmaneuver a faster but less nimble heat-seeking missile. The Homicidal Chauffeur was just one of many problems that RAND was exploring while developing the foundations of Game Theory, the study of how people and organizations make decisions where success depends not just on your own decisions, but on anticipating and responding to what others will do.

Much of RAND’s Game Theory funding came from the U.S. Department of Defense and the Air Force, who wanted to apply Game Theory to nuclear deterrence, cybernetic weapons systems, and conflict resolution. The most famous concept to emerge from RAND’s Game Theory work was Mutually Assured Destruction (MAD). RAND came to the conclusion that nations armed with nuclear weapons would avoid striking first against any other nuclear-armed nation that they knew would automatically respond with a nuclear counterstrike.

During the Kennedy administration, Defense Secretary Robert McNamara adopted MAD as official U.S. policy. He was telling Russia: “If you kill us, you will die, too.”

Stanley Kubrick’s Dr. Strangelove or: How I Learned to Stop Worrying and Love the Bomb (1964) was a satirical take on MAD as a nuclear deterrence strategy. Kubrick based the character of Dr. Strangelove on RAND Corporation theorists, and had extensively researched nuclear strategy. He originally planned to make a serious film but concluded that the logic of MAD was so bizarre that the concept could only be conveyed through satire.

WarGames (1983) was also about MAD and the danger of automated response systems. Its famous ending line was, "The only winning move is not to play." But how do you prevent the other player from making the first move, which forces you to play? That’s the point of how Mutually Assured Destruction works — by letting the enemy know you have an automated retaliation system that assures devastation, you can make sure the first move is never appealing to a rational opponent. (MAD doesn’t work against a suicidal opponent, obviously.)

In 2020, Javier Garcia and Professor Aaron T. Becker at the University of Houston created an interactive simulation of the Homicidal Chauffeur, which Becker described on YouTube:

The Hamstrung Squad Car

In his same 1951 paper, Isaacs described a similar, but simpler problem, which he called “The Hamstrung Squad Car.” (You have to hand it to him for coming up with attention-grabbing names for math problems!) This problem was revisited by Martin Gardner in his 1975 book, Mathematical Carnival. Here’s how he described it:

Imagine a city of infinite extent, with streets that form a regular square lattice. A squad car is at one intersection. At another is a carful of criminals. The squad car moves twice as fast as the criminals' car but is hamstrung by having to observe municipal traffic rules that prohibit left turns and U-turns, so that it can only go straight ahead or turn right at each intersection; the criminals' car does not observe these restrictions, so that at each intersection it can move in any of the four directions.

The problem to solve:

From what starting positions can the criminals be captured? Isaacs shows that surrounding the squad car's initial square there is an asymmetrical, compact area of exactly 69 squares, each of which is a fatal starting spot for the criminals.

The reader is urged to draw a large checkerboard of, say, 50 squares by 50 (or find a room with a suitable floor pattern), choose a starting position near the center for the squad car, and see if he can identify the 69 fatal squares.

Try the Hamstrung Car simulator

Here’s a Hamstrung Squad Car simulation I made (with coding help from AI). Give it a try, both in the manual and auto mode (for either or both cars). It’s a work in progress. Neither the squad car nor the crook car is using an optimal strategy. My goal is to have it run continuously until it finds the 69 safe squares. You are welcome to clone the GitHub repository to improve the project, or ask me for an invitation to work directly in my repository.

Thanks so much for supporting The Magnet, and I wish you a happy holiday!

Edited by Carla Sinclair